Suite de Fibonacci : mathématiques, symbolique & nature

Fibonacci et l’histoire d’une suite

Leonardo de Pise, plus connu sous le nom de Fibonacci, naît vers 1170 dans une Italie en pleine effervescence commerciale.
Fils d’un marchand pisan installé en Afrique du Nord, il découvre très tôt le système de numération arabe, infiniment plus pratique que les lourds chiffres romains.
Ce simple héritage changera la face de l’Europe : en 1202, dans son Liber Abaci (Le Livre de l’abaque), Fibonacci introduit pour la première fois de manière systématique les chiffres indo-arabes et la notion du zéro.
On mesure rarement à quel point ce geste fut une révolution : toute la comptabilité, l’algèbre, les calculs scientifiques modernes reposent sur cette bascule culturelle.

Au cœur de ce traité, destiné à enseigner aux marchands un calcul plus efficace, se glisse un problème en apparence anodin : celui de la reproduction de lapins, en couples idéalisés qui se multiplient mois après mois.
La solution qu’il propose engendre une suite d’entiers, où chaque terme est la somme des deux précédents : 0, 1, 1, 2, 3, 5, 8, 13…
Cette suite, qui portera son nom bien plus tard, n’était qu’un exercice parmi d’autres, une curiosité mathématique nichée dans un manuel pratique.

Mais l’histoire en décida autrement.
Car derrière ce jeu de lapins se cache une structure d’une puissance insoupçonnée : une suite simple à écrire, mais dont les ramifications touchent aux mathématiques les plus avancées, à la biologie, à l’architecture, à la musique et, par-delà la science, à la symbolique des civilisations.

La rigueur mathématique

La suite de Fibonacci se définit de manière récurrente :

Chaque terme est donc la somme des deux précédents.
Rien de plus simple à énoncer, mais cette simplicité cache une richesse infinie.
Dès les premiers calculs, une régularité se dessine : les rapports successifs entre deux termes consécutifs convergent peu à peu vers une valeur irrationnelle, environ 1,618…, que nous connaissons sous le nom de nombre d’or (φ).
Ce nombre, qui ne peut s’exprimer comme une fraction exacte, possède une propriété singulière :

Autrement dit, il se reproduit dans sa propre définition.
Cette auto-similarité fascina aussi bien les mathématiciens que les artistes et les mystiques.

La suite de Fibonacci peut également être exprimée grâce à une formule explicite, connue sous le nom de formule de Binet, qui fait intervenir le nombre d’or et son conjugué :

Cette expression permet de calculer directement le n-ième terme sans passer par la récurrence, et illustre la profondeur cachée de la suite.

Le lien avec le nombre d’or ne fut pourtant pas établi par Fibonacci lui-même : il apparaît seulement à la Renaissance, lorsque les mathématiciens et les artistes (re)découvrent les proportions harmonieuses.

Ainsi, sous ses dehors naïfs, la suite de Fibonacci devient un pont entre l’arithmétique élémentaire et des structures plus profondes : équations différentielles, matrices, théorie des nombres.
Dans son apparente simplicité, elle ouvre les portes de l’infini mathématique.

Fibonacci dans la nature et l’art

La nature, un livre écrit en spirales

On pourrait croire que la suite de Fibonacci est un simple jeu abstrait. Mais dès qu’on regarde autour de nous, on découvre qu’elle façonne le monde vivant.

• Phyllotaxie des plantes :
  Les feuilles, bourgeons et pétales ne s’agencent pas au hasard.
  Chez les tournesols, les graines forment deux spirales entremêlées, dont le nombre correspond précisément à deux termes successifs de Fibonacci (34 et 55, ou 89 et 144). Ce schéma optimise l’espace et la captation de la lumière.

• Pommes de pin et ananas :
  Leurs écailles s’enroulent selon des spirales ascendantes, visibles à l’œil nu.
  Là encore, le comptage donne deux nombres de la suite.
  
• Coquillages et cornes animales :
  La coquille du nautile, les escargots ou encore les cornes de certains béliers croissent en spirale logarithmique.
  La suite de Fibonacci n’est pas directement « inscrite » dans la forme, mais elle en sous-tend la logique de croissance.
  
• Au-delà du vivant :
  On retrouve cette structure dans les cyclones et les galaxies spirales, comme si l’univers lui-même écrivait ses formes en suivant une règle de proportion universelle.

Arts et architecture

La Renaissance fut l’un des moments privilégiés où les proportions issues de la suite de Fibonacci rencontrèrent l’idéal esthétique. On parlait alors de proportion divine : une harmonie censée refléter la perfection du cosmos.

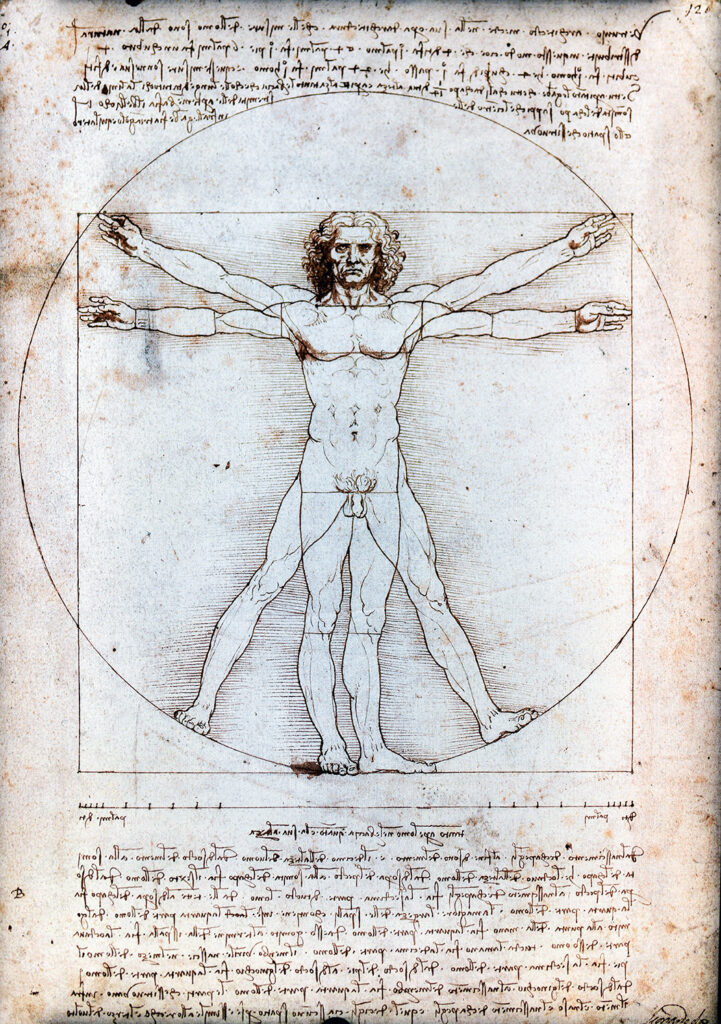
Léonard de Vinci illustra cette recherche en croquant l’Homme de Vitruve, figure inscrite dans le cercle et le carré, incarnation du rapport entre microcosme et macrocosme.
Ses travaux sur l’anatomie, la peinture ou l’architecture s’appuient sur des rapports numériques qui évoquent le nombre d’or et les suites qui y conduisent.

Les bâtisseurs de la Renaissance, héritiers des mathématiciens grecs, intégrèrent ces proportions dans les façades, les coupoles et les places. L’œil y perçoit un équilibre, un ordre qui dépasse la simple utilité.

La musique elle-même n’échappe pas à cette logique : certaines compositions classiques s’organisent en phrases dont les rapports de durée suivent la suite de Fibonacci, produisant une sensation d’équilibre presque naturelle.

Ainsi, de la peinture à l’architecture en passant par la musique, la suite de Fibonacci et le nombre d’or devinrent des repères essentiels pour penser l’harmonie.
L’Homme de Vitruve de Léonard de Vinci en offre l’illustration la plus célèbre : le corps humain y est inscrit à la fois dans un carré et dans un cercle.
Le carré, associé à la Terre et au monde matériel, dialogue avec le cercle, symbole du cosmos et de l’infini.
Entre les deux, l’homme devient médiateur, reliant la rigueur terrestre à l’ordre universel.

Symbolique universelle : harmonie, équilibre, ordre caché

La suite de Fibonacci ne se limite pas à un jeu numérique ou à une commodité géométrique.
Elle traduit quelque chose de plus fondamental : l’aspiration humaine à découvrir, derrière le chaos apparent, un ordre caché.

Chaque terme engendré par la relation simple Fₙ = Fₙ₋₁ + Fₙ₋₂ évoque une logique de filiation, où le nouveau naît toujours de la rencontre du passé.
Une métaphore du temps, mais aussi de la mémoire collective.

Dans la tradition symbolique, cette suite a souvent été rapprochée du nombre d’or, φ, perçu comme mesure d’équilibre et d’harmonie.
Là où les proportions ordinaires paraissent arbitraires, φ introduit une forme de nécessité qui transcende les cultures : de la Grèce antique aux artistes de la Renaissance, des architectes sacrés aux géomètres modernes, l’idée que la beauté s’accorde à une loi universelle revient sans cesse.

Plus encore, la spirale de Fibonacci est devenue l’une des images archétypales de cette quête.
Elle exprime à la fois le déploiement infini et le retour cyclique, le mouvement qui s’élargit sans jamais rompre son origine. Elle condense deux visions du monde : l’expansion et la reliance.

C’est peut-être là sa force : nous rappeler que le monde n’est pas fait uniquement de discontinuités, mais de correspondances.
Que la rigueur mathématique et la symbolique poétique ne s’excluent pas, mais se complètent.
Que l’harmonie véritable se loge dans la tension féconde entre raison et imaginaire.

Cette harmonie, que l’on retrouve dans les plantes, les coquillages ou les galaxies, ne se limite pas aux formes les plus grandioses.
Elle habite aussi le détail le plus infime, comme si le vivant tout entier obéissait à une logique commune.
La spirale de Fibonacci apparaît ainsi là où on ne l’attend pas : dans le simple enroulement de la queue d’un caméléon, fragile miracle de géométrie vivante.

Un outil de pensée et d’ancrage

Dimension symbolique

La spirale de Fibonacci ne se contente pas d’illustrer un calcul élégant.
Elle s’impose comme un symbole puissant, image du temps qui s’écoule, des cycles qui se répètent et du déploiement continu du vivant.
Elle suggère à la fois le retour à l’identique et l’ouverture vers l’infini, un mouvement qui englobe mémoire et devenir.

Dans la tradition des arts libéraux, ce motif relie les disciplines entre elles : la mathématique y trouve sa pureté, la musique son rythme, la géométrie ses proportions.
Tout comme le trivium et le quadrivium formaient autrefois une grille de lecture du monde, la suite de Fibonacci incarne une logique universelle, un langage caché derrière les formes et les sons.

Dimension personnelle

Pour moi, la suite de Fibonacci n’est pas seulement une élégance mathématique ou un symbole universel. Elle est aussi un outil de survie.
Quand une de ces crises d’angoisse violentes, disproportionnées, dont beaucoup d’autistes sont coutumiers, me submerge, je trouve dans ces nombres une planche de salut.

Je repars du début : zéro, un, un, deux, trois, cinq, huit…
Chaque terme qui surgit en appelle un autre, comme si la logique des lapins médiévaux de Fibonacci venait me tirer hors du chaos.
C’est un fil d’Ariane numérique, une corde tendue entre l’abstraction et le réel.

En récitant la suite, je me raccroche au monde physique, à sa cohérence sous-jacente.
Les chiffres deviennent un rythme, presque un battement.
Et peu à peu, l’ordre reprend le dessus, l’angoisse reflue. Là où d’autres prient, méditent ou se taisent, je compte.
Et dans ce décompte se loge ma manière de m’ancrer dans le monde physique.

Ainsi, ce qui fut pour moi d’abord un simple outil de survie devient aussi, plus largement, un repère concret. Le calcul rejoint l’existence.
Dans la simplicité de la suite (pas si simple à calculer de tête en pleine crise de panique quand même), certains trouvent un fil qui les relie au réel, un point fixe dans l’instabilité des choses.
La spirale devient alors une méditation incarnée, une manière de tenir le monde entre ses mains, en chiffres, en rythme, en souffle.

Politique du nombre

Ce que le capitalisme a détruit

Le capitalisme a réduit le savoir à un outil, une marchandise, une compétence mesurée à l’aune de son rendement.
Les sciences ne valent plus que si elles « servent » à produire, innover, breveter, vendre. Les humanités ne valent plus rien.
Et la connaissance est devenue un simple passeport pour « gagner sa vie » (expression ignoble qui suppose qu’on ne vivrait pas déjà, qu’il faudrait payer sa respiration à l’usine).

Dans ce monde rabougri, le lien entre la science, le cosmos et le sens s’est rompu.
Nous n’apprenons plus pour comprendre, mais pour exécuter.
Nous ne cherchons plus l’harmonie, mais le profit.
Le savoir a été mutilé, tronqué, réduit à un mode d’emploi.

Ce que la suite nous rappelle

La suite de Fibonacci, elle, n’a pas de fonction utilitaire immédiate.
Elle ne sert à rien et c’est précisément pour cela qu’elle est précieuse.
Elle nous rappelle que la connaissance est d’abord gratuite, qu’elle vaut pour la beauté qu’elle révèle, non pour le profit qu’elle génère.

Elle nous rappelle aussi l’harmonie et l’interdépendance dans la nature : les spirales végétales, les proportions du corps, les galaxies entières rappellent que l’univers n’est pas une somme de fragments, mais un tissu.
Tout est lié.

Enfin, elle nous impose une leçon politique : repenser nos logiques sociales et économiques non pas en termes de croissance et de marges, mais en termes d’équilibre.
Un équilibre entre la nature et l’homme, entre la science et la poésie, entre l’utilité et la gratuité.

Conclusion

La suite de Fibonacci n’est pas qu’une curiosité mathématique.
Elle est une clé, un pont jeté entre science et symbolique, entre rigueur et imaginaire.
Elle montre qu’il existe un ordre caché derrière le désordre apparent, que le cosmos et la culture se répondent.

En elle se croisent l’héritage des Anciens, l’audace de la Renaissance, l’observation de la nature et le besoin humain d’harmonie.
Elle prouve que les nombres ne sont pas seulement des outils, mais des vecteurs de sens.

À l’heure où le capitalisme piétine la gratuité du savoir et réduit la pensée à un tableau Excel, la suite de Fibonacci nous rappelle une évidence : comprendre le monde, c’est déjà transformer notre manière d’y vivre.

Et c’est aussi une invitation à relier les fils : de la spirale de Fibonacci aux arts libéraux, du nombre d’or au trivium et au quadrivium, une même logique se dessine, celle d’une pensée qui refuse d’être mutilée.

Vous trouvez ça excessif ?
Parfait.
Ça me fait plaisir de vous avoir fait réagir.

Léon

Léon Chelli arpente les mondes de l’automobile et des énergies renouvelables à travers la transition écologique. Il y déchiffre mutations industrielles et stratégies de marché avec la lucidité un peu sauvage d’un promeneur qui choisit ses propres sentiers.
Il explore les transitions avec une vision systémique, entre ironie assumée et clarté analytique.